With Racket chosen as our implementation language, and the translations for the Turtle Procedure Notation’s language constructs worked out, there’s only one thing left before we can start interacting with the Turtle: the Turtle control functions. This post will focus on their implementation.

Preamble

Imagine that you have control of a little creature called a turtle that exists in a mathematical plane or, better yet, on a computer display screen. The turtle can respond to a few simple commands: FORWARD moves the turtle, in the direction it is facing, some number of units. RIGHT rotates it in place, clockwise, some number of degrees. BACK and LEFT cause the opposite movement.

I came across this book: Turtle Geometry: The Computer as a Medium for Exploring Mathematics by Harold Abelson and Andrea diSessa¹, which describes itself as “a computer-based introduction to geometry and advanced mathematics at the high school or undergraduate level”, and thought it would be fun to work through it generating the images, and doing the exercises.

I’m implementing it in Racket, but the Turtle Procedure Notation used in the book is quite easy to adapt to any language.

If you’d like to follow along, there is an open access edition of the book available here: MIT Press Direct: Turtle Geometry.

The previous post in this Turtle Geometry series can be found here.

1. Introduction to Turtle Geometry

This chapter is an introduction on three levels. First, we introduce you to a new kind of geometry called turtle geometry. The most important thing to remember about turtle geometry is that it is a mathematics designed for exploration, not just for presenting theorems and proofs. When we do state and prove theorems, we are trying to help you to generate new ideas and to think about and understand the phenomena you discover.

The technical language of this geometry is our second priority. This may look as if we’re describing a computer language, but our real aim is to establish a notation for the range of complicated things a turtle can do in terms of the simplest things it knows.

Finally, this chapter will introduce some of the important themes to be elaborated in later chapters. These themes permeate not only geometry but all of mathematics, and we aim to give you rich and varied experiences with them.

1.1 Turtle Graphics

At this point we revisit the quote I used in the preamble:

Imagine that you have control of a little creature called a turtle that exists in a mathematical plane or, better yet, on a computer display screen. The turtle can respond to a few simple commands: FORWARD moves the turtle, in the direction it is facing, some number of units. RIGHT rotates it in place, clockwise, some number of degrees. BACK and LEFT cause the opposite movement.

Figure 1.1

The book then presents Figure 1.1: A sequence of turtle commands. Looking at Figure 1.1(a), p.4#fig.1.1a we see that the turtle is pointing straight up, whereas when we run:

#lang racket

;; Prelude B.0
;;
;; Initialize Turtle Graphics.
(require graphics/turtles)
(turtles #t)

our turtle is pointing towards the right. Let’s fix that, and add it to our prelude:

;; Prelude 1.0, p.4#fig.1.1a
;;
;; Rotate Turtle to match book orientation. 
;;
(turn 90)

Figure 1.1 (a)

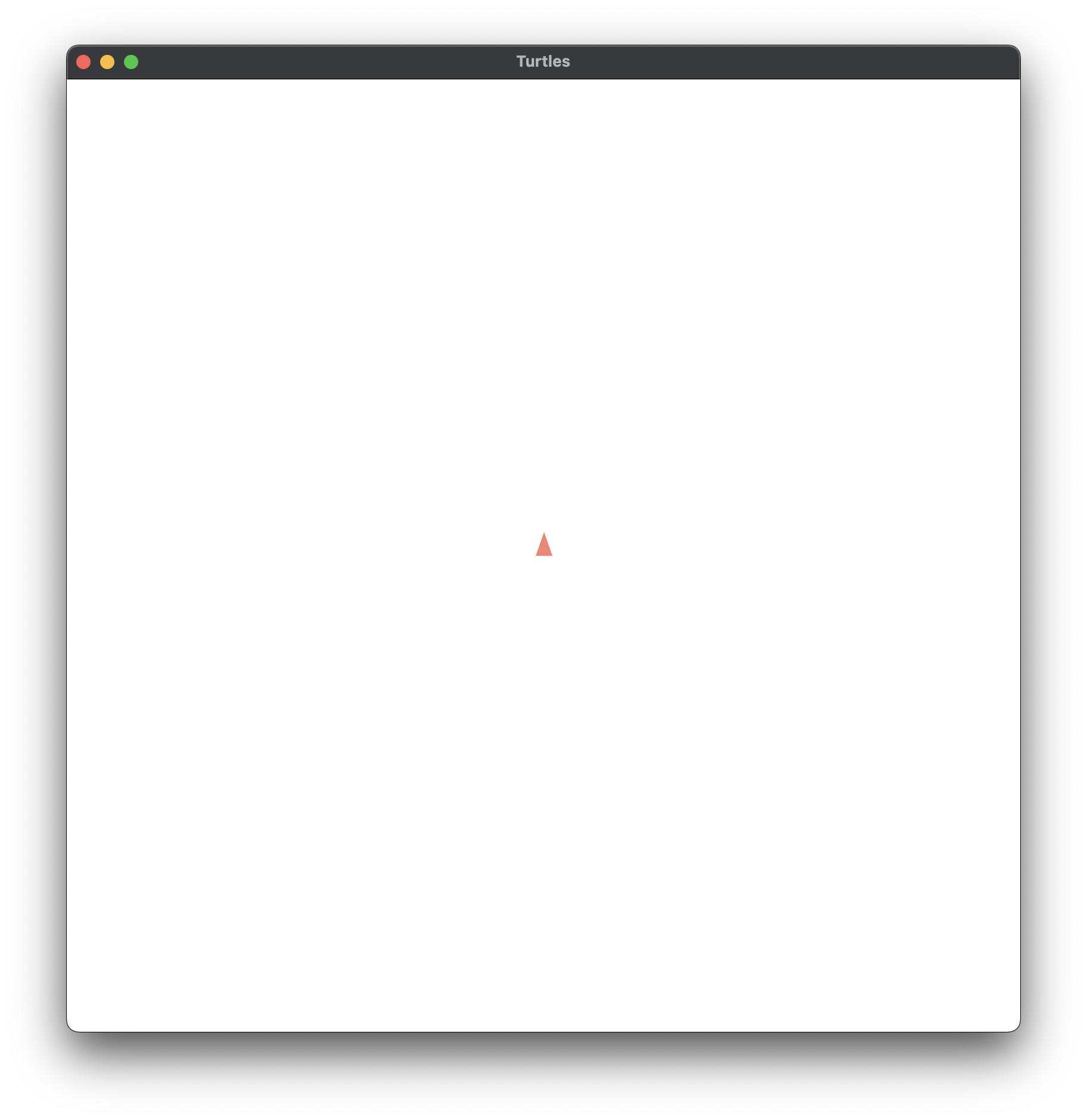
;; Figure 1.1a, p.4#fig.1.1a
;; 
;; ; Turtle starts
;;

The book describes 6 commands which control the turtle:

• FORWARD <units> — Formula 1.0, p.3#form.0
• BACK <units> — Formula 1.2, p.3#form.2
• RIGHT <degrees> — Formula 1.1, p.3#form.1
• LEFT <degrees> — Formula 1.3, p.3#form.3
• PENUP — Formula 1.4, p.4#form.0
• PENDOWN — Formula 1.5, p.4#form.1

The Turtle Graphics library we’re using has:

• (move n) — Moves the turtle n pixels without drawing.
• (draw n) — Moves the turtle n pixels and draws a line on the path.
• (turn theta) — Turns the turtle theta degrees counter-clockwise.

These are enough to provide the functionality described.

The turtle can leave a trace of the places it has been: The position- changing comands can cause lines to apear on the screen. This is controled by the comands PENUP and PENDOWN.

;; Hold the state of the pen '(up down).
(define pen-state 'down)

;; Prelude 1.1
;; Formula 1.4, p.4#form.0
;;
;; PENDOWN
;;
(define (pendown)
  (set! pen-state 'down))

;; Prelude 1.2
;; Formula 1.5, p.4#form.1
;;
;; PENUP
;;
(define (penup)
  (set! pen-state 'up))

First we deal with keeping track of whether the turtle’s pen is up or down, and make pendown and penup functions to change the state.

…FORWARD and BACK change the turtle’s position (the point on the plane where the turtle is located);

When the pen is down, the turtle draws lines.

;; Prelude 1.3
;; Formula 1.0, p.3#form.0
;;
;; FORWARD <units>
;;
(define (forward n)
  (case pen-state
    [(up) (move n)]
    [(down) (draw n)]))

;; Prelude 1.4
;; Formula 1.2, p.3#form.2
;;
;; BACK <units>
;;
(define (back n)
  (forward (- n)))

Here we make the turtle’s position functions forward and back, taking the pen’s state into consideration.

…RIGHT and LEFT change the turtle’s heading (the direction in which the turtle is facing).

;; Prelude 1.5
;; Formula 1.3, p.3#form.3
;;
;; LEFT <degrees>
;;
(define (left n)
  (turn n))

;; Prelude 1.6
;; Formula 1.1, p.3#form.1
;;
;; LEFT <degrees>
;;
(define (right n)
  (left (- n)))

And lastly we make the turtle’s heading functions left and right.

With those done we are able to generate all of the images in Figure 1.1, p 4#fig.1.1.

Figure 1.1 illustrates how you can draw on the display screen by steering the turtle with FORWARD, BACK, RIGHT, and LEFT.

Figure 1.1 (b)

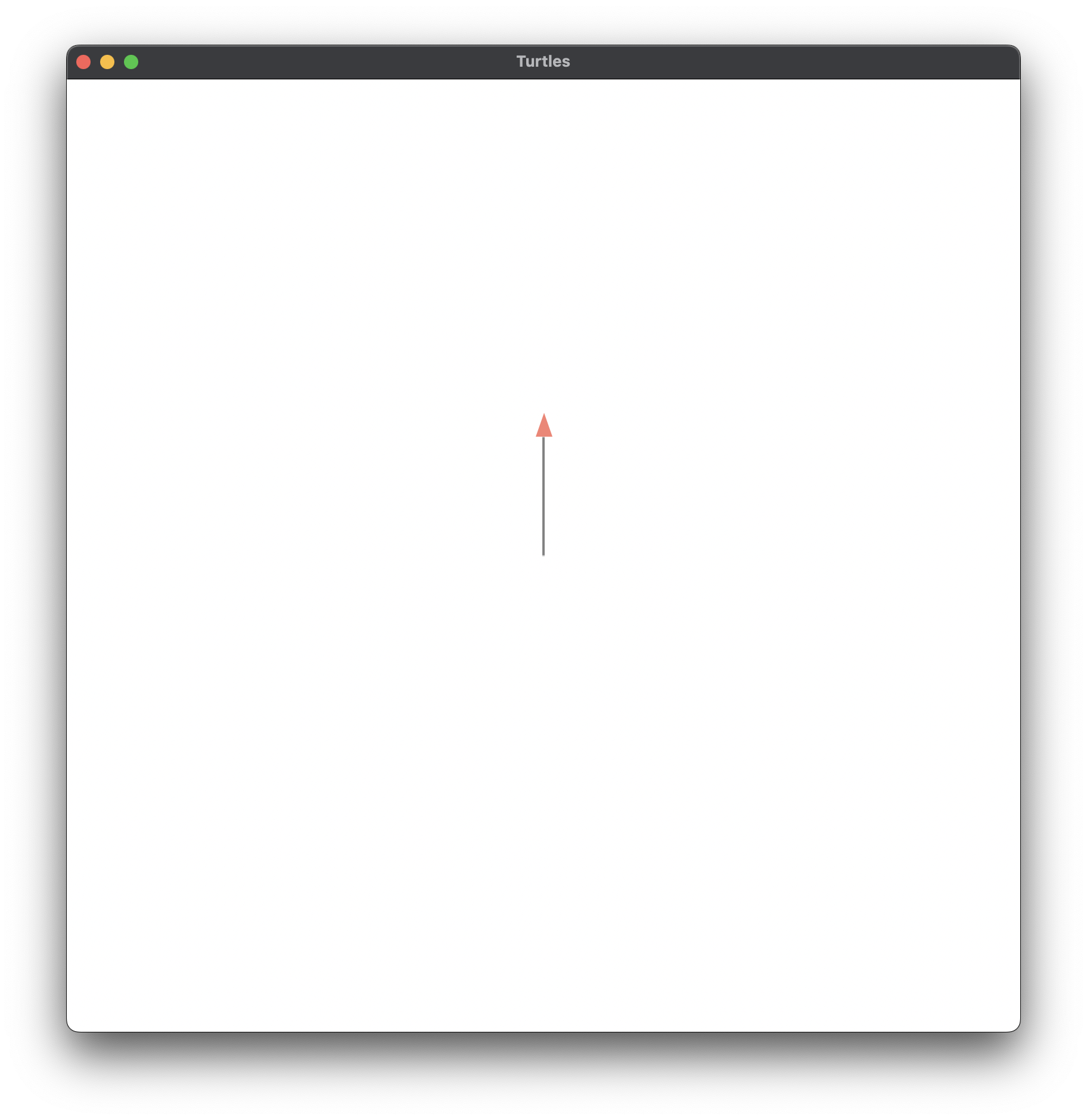
;; Figure 1.1b, p.4#fig.1.1b
;;
;; FORWARD 100
;;
(forward 100)

Figure 1.1 (c)

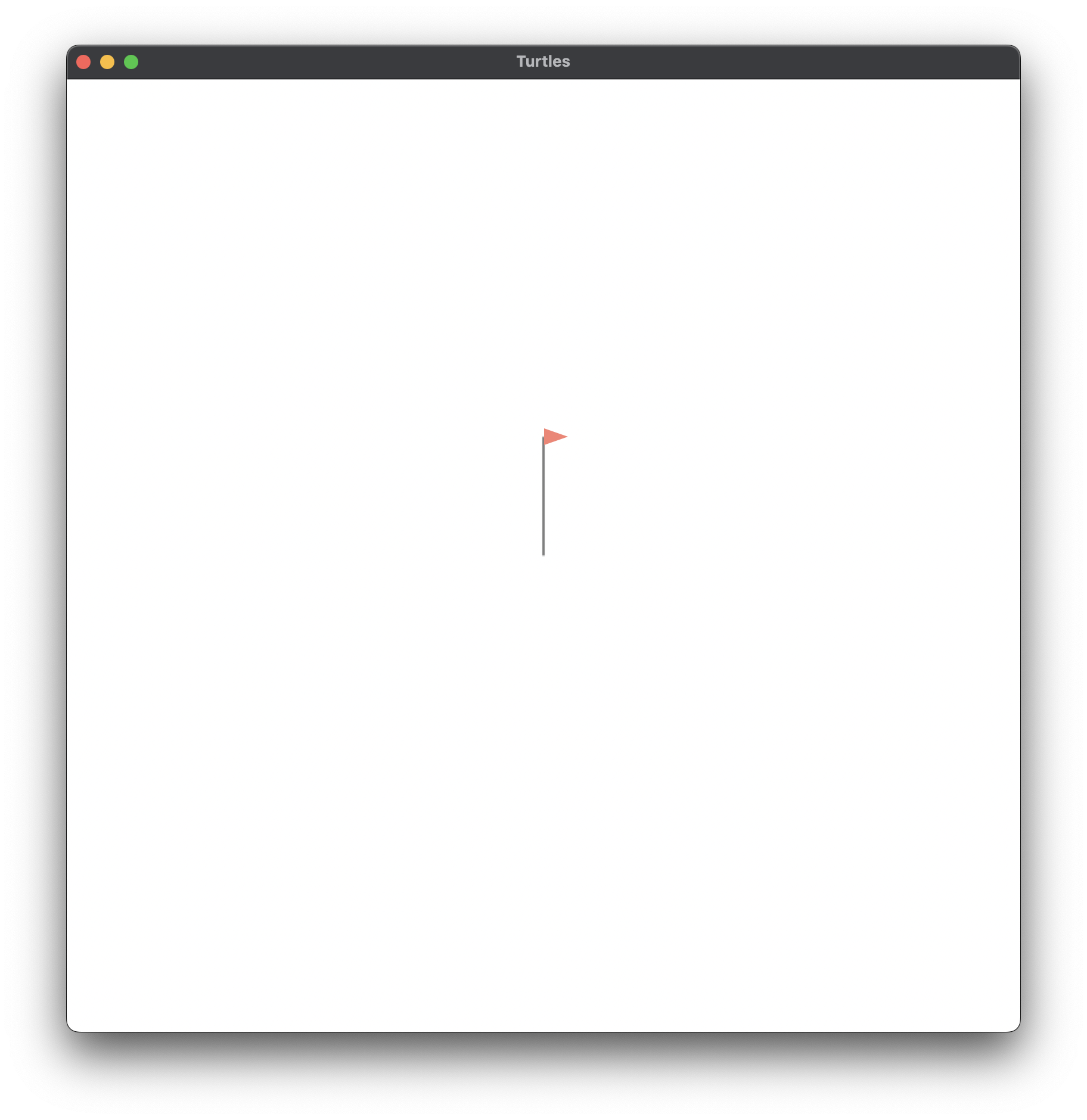
;; Figure 1.1c, p.4#fig.1.1c
;;
;; RIGHT 90
;;
(right 90)

Figure 1.1 (d)

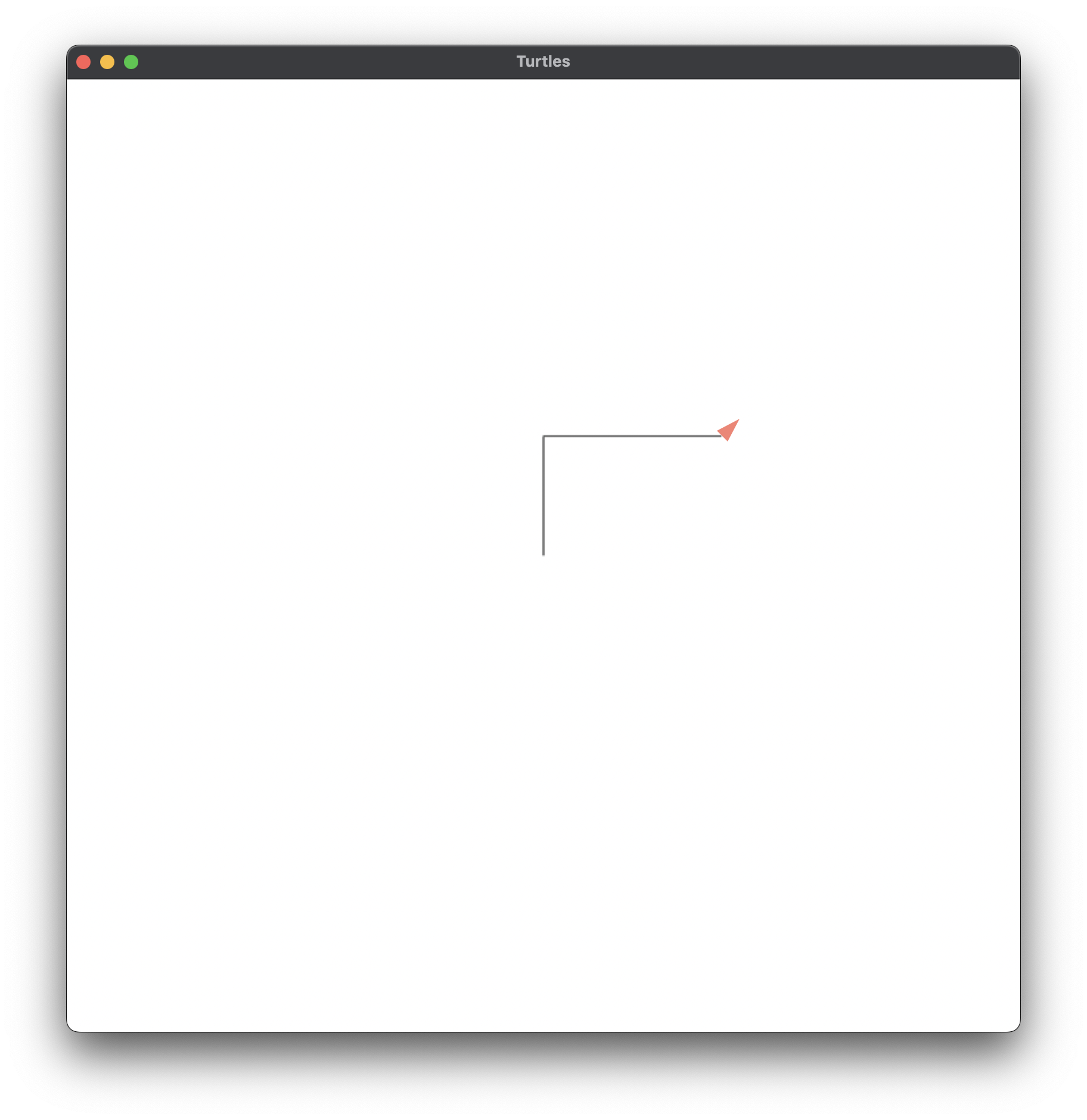
;; Figure 1.1d, p.4#fig.1.1d
;;
;; FORWARD 150
;; LEFT 45
;;
(forward 150)
(left 45)

Figure 1.1 (e)

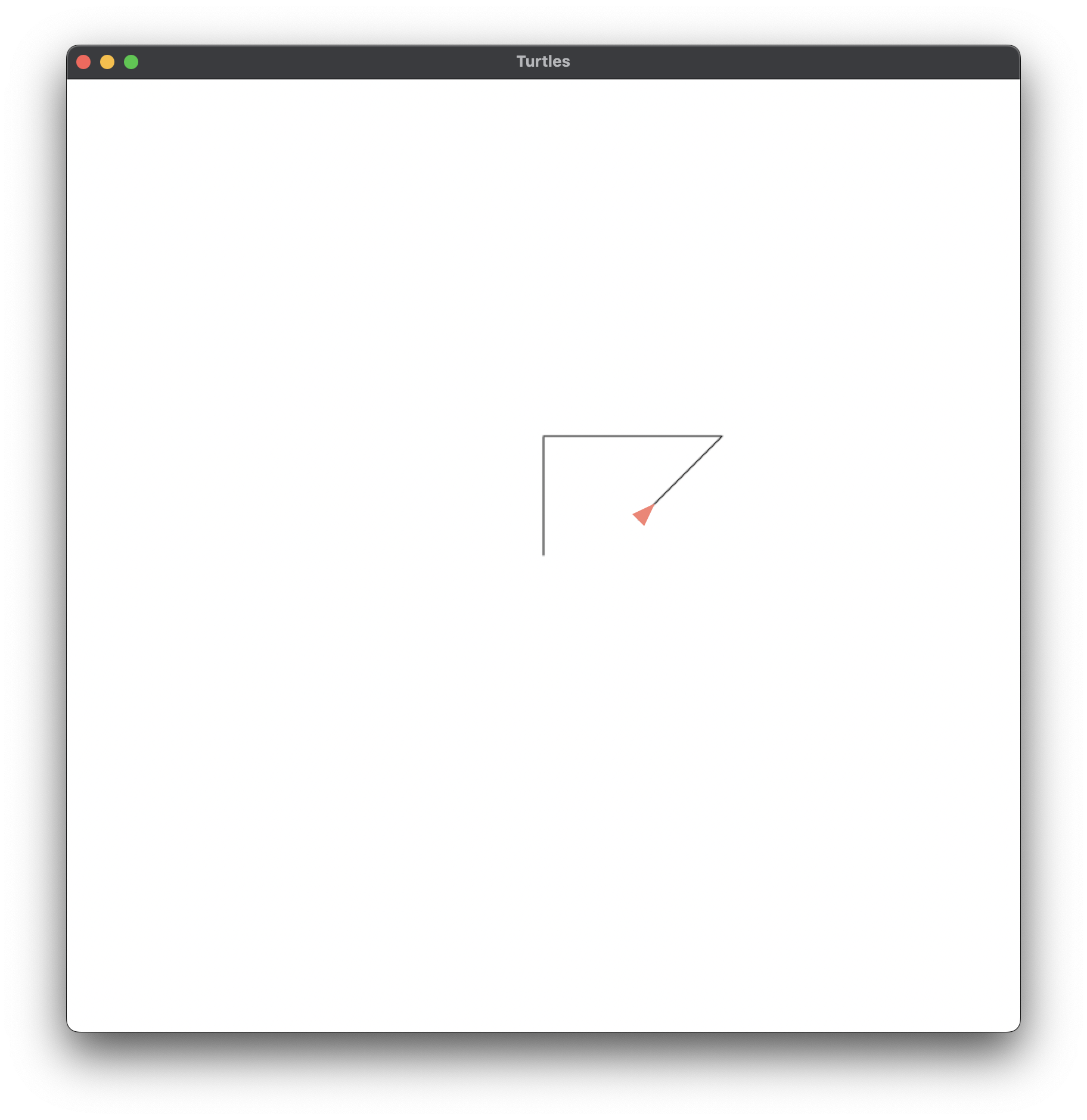
;; Figure 1.1e, p.4#fig.1.1e
;;
;; BACK 100
;;
(back 100)

Figure 1.1 (f)

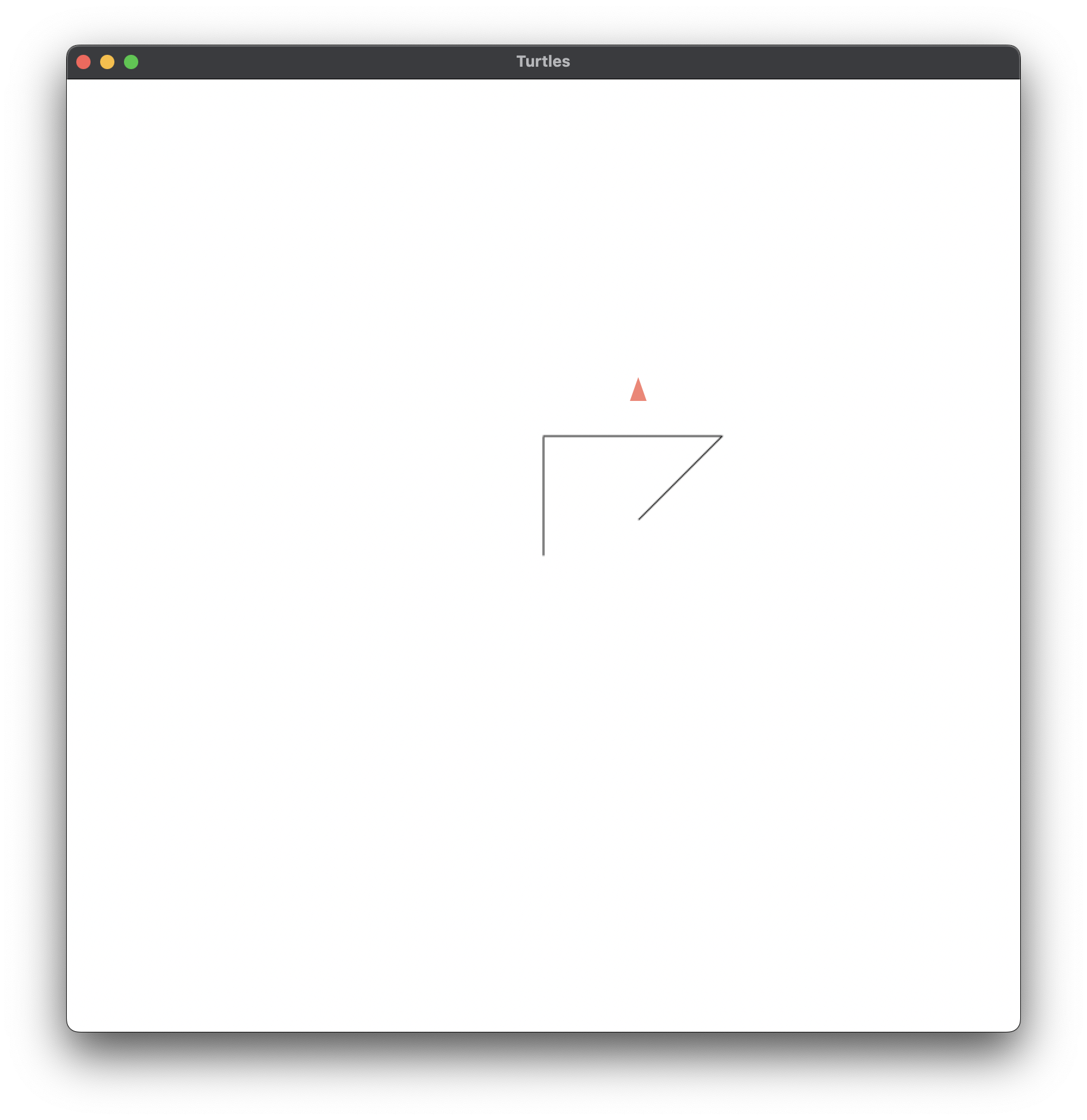
;; Figure 1.1f, p.4#fig.1.1f
;;
;; LEFT 45
;; PENUP
;; FORWARD 100
;;
(left 45)
(penup)
(forward 100)

Reflections

That was fun, we’ve got the turtle moving, and have replicated our first series of images. The code is available as chapter-1.1.rkt in the blog’s accompanying turtle-geometry-racket repository on GitHub.

Next Steps

We’ve set up the Turtle Geometry environment, implemented some turtle control functions, and drawn a few simple pictures.

In the next post we’ll get an introduction to the Turtle Graphics Notation’s procedures, and we’ll use them, the turtle control functions from this post, and the language constructs from the previous post to draw a few more simple pictures as we familiarise ourselves with the notation.