Now that we have the Turtle Geometry environment set up, implemented some turtle control functions, and used them to draw a few simple pictures, it’s time to become familiarised with the Turtle Procedure Notation for procedures and iteration.

Preamble

Imagine that you have control of a little creature called a turtle that exists in a mathematical plane or, better yet, on a computer display screen. The turtle can respond to a few simple commands: FORWARD moves the turtle, in the direction it is facing, some number of units. RIGHT rotates it in place, clockwise, some number of degrees. BACK and LEFT cause the opposite movement.

I came across this book: Turtle Geometry: The Computer as a Medium for Exploring Mathematics by Harold Abelson and Andrea diSessa¹, which describes itself as “a computer-based introduction to geometry and advanced mathematics at the high school or undergraduate level”, and thought it would be fun to work through it generating the images, and doing the exercises.

I’m implementing it in Racket, but the Turtle Procedure Notation used in the book is quite easy to adapt to any language.

If you’d like to follow along, there is an open access edition of the book available here: MIT Press Direct: Turtle Geometry.

The previous post in this Turtle Geometry series can be found here.

1.1.1 Procedures

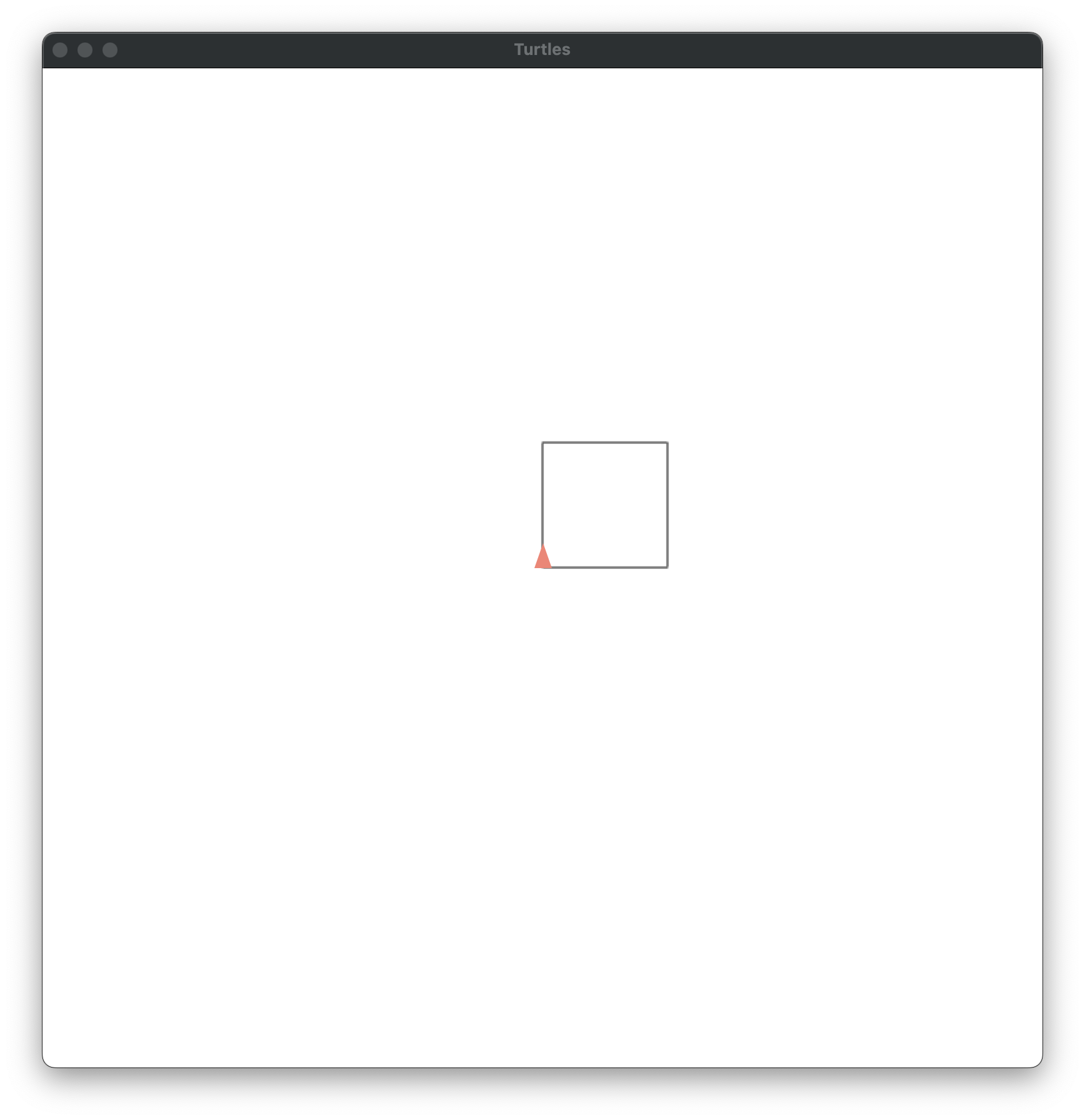
Turtle geometry would be rather dull if it did not allow us to teach the turtle new commands. But luckily all we have to do to teach the turtle new tricks is to give it a list of commands it already knows. For example, here’s how to draw a square with sides 100 units long:

Computation 1.1.1.0

An example of a procedure. The first line of the procedure (the title line) specifies the procedure’s name. The rest of the procedure (the body) specifies a list of instructions the turtle is to carry out in response to a SQUARE command.

;; Computation 1.1.1.0, p.5#comp.0
;; 
;; TO SQUARE
;;    FORWARD 100
;;    RIGHT 90
;;    FORWARD 100
;;    RIGHT 90
;;    FORWARD 100
;;    RIGHT 90
;;    FORWARD 100
;;    RIGHT 90
;;
(define (square)
  (forward 100)
  (right 90)
  (forward 100)
  (right 90)
  (forward 100)
  (right 90)
  (forward 100)
  (right 90))

To call the procedure issue the procedure’s name as a command, in this case SQUARE.

Example 1.1.1.0

Response to a SQUARE command.

;; Example 1.1.1.0, p.5#ex.0
;; 
;; SQUARE
(square)

---

There are a few useful tricks for writing procedures. One of them is called iteration, meaning repetition—doing something over and over. Here’s a more concise way of telling the turtle to draw a square, using iteration:

Computation 1.1.1.1

Repeat the indented commands FORWARD 100 and RIGHT 90 four times.

;; Computation 1.1.1.1, p.5#comp.1
;; 
;; TO SQUARE
;;    REPEAT 4
;;       FORWARD 100
;;       RIGHT 90
;;
(define (square)
  (repeat 4
    (forward 100)
    (right 90)))

Another trick is to create a SQUARE procedure that takes an input for the size of the square.

Computation 1.1.1.2

A SQUARE procedure that takes an input for the size of the square.

;; Computation 1.1.1.2, p.5#comp.2
;;
;; TO SQUARE SIZE
;;    REPEAT 4
;;       FORWARD SIZE
;;       RIGHT 90
;;
(define (square size)
  (repeat 4
    (forward size)
    (right 90)))

Now, when you use the command, you must specify the value to be used for the input, so you say SQUARE 100, just like FORWARD 100.

Example 1.1.1.1

Response to a SQUARE 100 command.

;; Example 1.1.1.1, p.6#ex.0
;; 
;; SQUARE 100
(square 100)

---

The chunk FORWARD SIZE, RIGHT 90 might be useful in other contexts, which is a good reason to make it a procedure in its own right:

;; Computation 1.1.1.3, p.6#comp.0
;;
;; TO SQUAREPIECE SIZE
;;    FORWARD SIZE
;;    RIGHT 90
;;
(define (squarepiece size)
  (forward size)
  (right 90))

Now we can rewrite SQUARE using SQUAREPIECE as

;; Computation 1.1.1.4, p.6#comp.1
;;
;; TO SQUARE SIZE
;;    REPEAT 4
;;      SQUAREPIECE SIZE
;;
(define (square size)
  (repeat 4 (squarepiece size)))

SQUAREPIECE can be used as a subprocedure in other places as well—for example, in drawing a rectangle:

;; Computation 1.1.1.5, p.6#comp.2
;; 
;; TO RECTANGLE SIDE1 SIDE2
;;    REPEAT 2
;;       SQUAREPIECE SIDE1
;;       SQUAREPIECE SIDE2
;;
;; Computation 1.1.1.6, p.6#comp.3
;; 
;; TO RECTANGLE (SIDE1, SIDE2)
;;    REPEAT 2
;;       SQUAREPIECE (SIDE1)
;;       SQUAREPIECE (SIDE2)
;;
(define (rectangle side1 side2)
  (repeat 2
          (squarepiece side1)
          (squarepiece side2)))

To use the RECTANGLE procedure you must specify its two inputs, for example, RECTANGLE 100 50.

Example 1.1.1.2

Rectangle.

;; Example 1.1.1.2, p.6#ex.1
;;
;; RECTANGLE 100 50
;;
(rectangle 100 50)

---

Reflections

The conversion to Racket was straightforward, the code is available as chapter-1.1.1.rkt in the blog’s accompanying turtle-geometry-racket repository on GitHub.

Next Steps

We’ve explored how to generate and call procedures with parameters, and perform iteration. Along we way we’ve generated a few boxy images.

In the next post we’ll continue on our introduction to the language, with the focus on drawing.